In the world of mathematics and physics, the 2D cross product might not be the star of the show, but it certainly deserves a standing ovation. This nifty little operation packs a punch, turning two-dimensional vectors into a single scalar value that can reveal a lot about their relationship. Think of it as the secret sauce that adds flavor to vector calculations, making them not just palatable but downright delicious.
Table of Contents
ToggleUnderstanding The 2D Cross Product
The 2D cross product simplifies vector analysis by producing a single scalar value. This scalar reveals essential information about the relationship between two vectors in a plane.
Definition and Importance
The 2D cross product occurs between two vectors represented as ((x_1, y_1)) and ((x_2, y_2)). Mathematically, the cross product is defined as (z = x_1y_2 – y_1x_2), where (z) denotes the resulting scalar. This operation is vital in applications within physics and engineering, as it helps determine the area of the parallelogram formed by the vectors. Additionally, it indicates the orientation of the vectors relative to one another, which is crucial for tasks such as calculating torque and angular momentum.
Geometric Interpretation
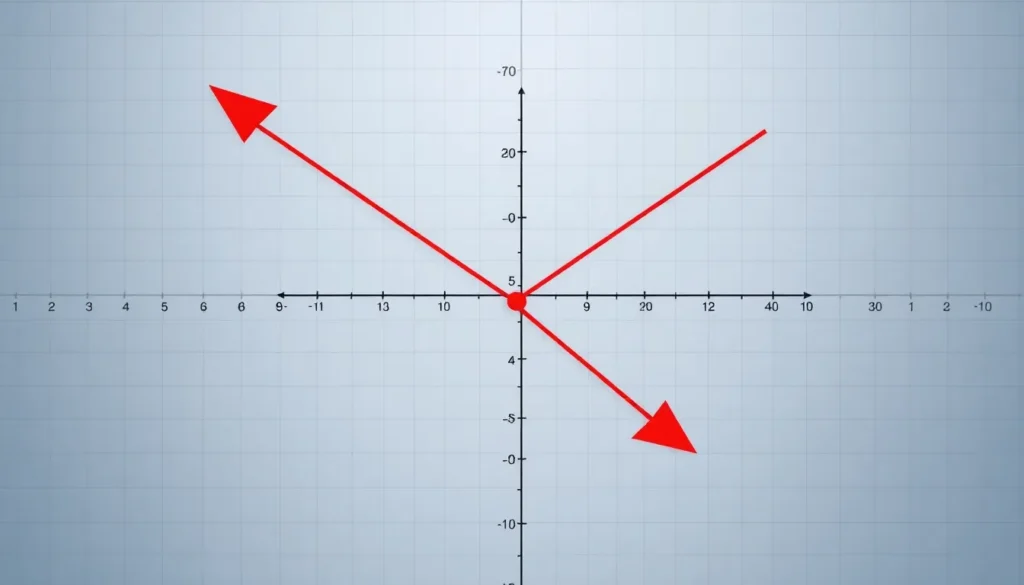
Geometrically, the 2D cross product represents the area of the parallelogram formed by two vectors. Vectors can be visualized as arrows extending from a common point, and the cross product quantifies the space enclosed between them. The sign of the result indicates the direction of rotation, with a positive value suggesting a counterclockwise turn and a negative value indicating a clockwise turn. This intuitive interpretation aids in comprehending concepts related to motion and force in two-dimensional systems. The relationship between the vectors and their resulting scalar can thus enhance insights into physical scenarios.
Mathematical Formulation

The 2D cross product operates primarily with two-dimensional vectors, resulting in a scalar value. This capability provides insights into vector relationships within a plane.
Formula and Components
The formula for the 2D cross product is represented as ( z = x_1y_2 – y_1x_2 ). In this equation, ( (x_1, y_1) ) corresponds to the first vector, while ( (x_2, y_2) ) represents the second vector. The result, ( z ), conveys crucial information about the vectors’ orientation and the area of the parallelogram they enclose. When calculating, the order of the vectors significantly influences the outcome, as reversing them changes the sign of the scalar.
Computational Steps
To compute the 2D cross product, first identify the components of each vector. Next, multiply the x-component of the first vector by the y-component of the second vector. Following that, multiply the y-component of the first vector by the x-component of the second vector. Finally, subtract the second product from the first. This method provides the scalar result, offering insights into the relative direction and area defined by the two vectors.
Applications of 2D Cross Product
The 2D cross product has several important applications in various fields. Understanding these uses emphasizes the relevance of this mathematical operation.
Physics and Engineering
In physics and engineering, the 2D cross product aids in analyzing forces and moments acting on objects. Determining the torque generated by a force vector at a distance from a pivot point relies on this operation. The scalar result indicates the effectiveness of the force in causing rotation. Additionally, calculating the area of a shape formed by two vectors helps in structural analysis and design. Designers often use this information to ensure stability and strength in structures. Hence, professionals utilize the 2D cross product to simplify complex calculations in mechanics and structural engineering.
Computer Graphics and Robotics
Computer graphics often employ the 2D cross product to compute surface normals, crucial for lighting and shading in rendering images. These normals, derived from two vector edges of a polygon, assist in simulating realistic lighting effects. Additionally, in robotics, the 2D cross product facilitates the determination of relative orientations and positions of robotic arms. By computing the area defined by joint vectors, systems can optimize movement paths and ensure efficient operation. Designers leverage the insights from the 2D cross product to enhance realism and performance in graphical and robotic applications.
Common Misconceptions
Understanding the 2D cross product often leads to misunderstandings among learners. Clarifying these misconceptions enhances comprehension and application.
Difference Between 2D and 3D Cross Product
Confusion arises when comparing the 2D cross product to its 3D counterpart. The 2D version produces a scalar, while the 3D operation results in a vector. In 2D, the calculation focuses solely on the x and y components, producing a single value that indicates area and orientation. The 3D cross product, however, encodes directionality in three-dimensional space, yielding a vector that can point in any direction. This fundamental difference affects how each cross product is used in mathematical applications, particularly in physics and engineering.
Misinterpretation of Results
Misinterpretation of the scalar result from the 2D cross product occurs frequently. Some may presume that a non-zero result signifies parallel vectors; however, this interpretation is incorrect. A zero scalar indicates that the vectors are indeed parallel. Additionally, the sign of the scalar conveys orientation—positive indicates counterclockwise rotation, while negative signals a clockwise direction. Recognizing these nuances ensures accurate application of the 2D cross product in various scenarios, such as determining areas or analyzing vector relationships.
The 2D cross product stands out as a powerful tool in mathematics and physics. By transforming two-dimensional vectors into a scalar value, it reveals critical insights about their relationships. Its ability to indicate orientation and calculate the area of the parallelogram formed by the vectors is invaluable across various fields.
From physics to computer graphics and robotics, the applications of the 2D cross product enhance understanding and performance. Recognizing its significance and nuances ensures accurate analysis and effective problem-solving. Embracing this mathematical operation can lead to more profound insights in both theoretical and practical contexts.